On définit la vitesse d'un vaisseau par la distance de translation (mesurée par la longueur du plus court chemin entre deux cellules : deux cellules adjacentes (cote à cote ou en diagonale) étant distantes de 1) divisée par la période.
La vitesse d'une cellule par génération est notée usuellement c, par analogie avec la vitesse de la lumière.
En effet un vaisseau ne peut avoir une vitesse égale ou supérieure à c.

Voici une démonstration.

L'idée est de montrer que si une structure (groupe de cellules vivantes) est en dessous d'une diagonale (d0) de cellules à la génération t=0, elle sera en dessous de la diagonale suivante (d2) à la génération t=2.

 

d0	d2
	d0	d2
		d0	d2
			d0	d2
				d0

Choisissons les notations suivantes (en correspondance avec la figure précédente) :

a
	b	u	x
	m	c	v
		n	d
				e

  Hypothèse : A t=0, toutes les cellules vivantes sont situées en dessous de d₀.
 
Supposons que x est vivante à t=2.
x est nécessairement morte à t=1 (elle l'est à t=0, et elle ne peut naître à t=1 car tous ses voisines sont mortes à t=0).
Pour que la cellule x soit vivante à t=2, il faut donc qu'à t=1 elle ait eu exactement trois voisines vivantes.
Ces voisines vivantes à t=1 ne pouvaient être que u,c et v (les autres voisines sont mortes à t=1).
C'est donc que u et v sont nées à t=1. Puisqu'il leurs fallait trois voisines pour naître, il faut qu'à t=0 b,c et m ainsi que c,n et d aient été vivantes.
Or cela implique que c meurt à t=1, car elle a plus de 3 voisines vivantes (b,m,n et d) à t=0, on arrive donc à une contradiction.
 
Donc (puisque toutes les cellules de d₂ sont dans le cas de x) à t=2, toutes les cellules vivantes sont en dessous de d₂.

A t=0 le vaisseau est précisement en dessous de la diagonale d₀.
D'après le résultat précédent on sait qu'à t=2n, le vaisseau est nécessairement en dessous de la diagonale d_2n.

On suppose de plus que p est paire : on peut toujours se ramener à ce cas, car 2p est toujours paire est est aussi une période du vaisseau (pour un déplacement 2A, 2B).

La case grisée correspond au deux positions d'une même cellule (une de celles qui sont le plus en haut à droite du vaisseau) à t=0 et à t=P.
L'ombre correspond au vaisseau.
Il apparaît que la diagonale d2(A+B) se trouve juste au dessus du vaisseau après son déplacement de A cases horizontalement et de B cases verticalement.

Or (cf. figure) à t=p le vaisseau est exactement en dessous de la droite d_2(A+B) .

C'est donc que d_p est au dessus de d_2(A+B).
C'est à dire que :

P2(A+B)

Donc D(A+B).

On obtient alors  : V(A+B)/ (2 (A+B)) = 1/2.

En notant c la vitesse d'une case par génération, le résultat se met sous la forme :

V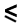 c/2

Le remplisseur du plan est la structure dont la vitesse de croissance est la plus élevée possible.

Cette structure à la propriété de s'agrandir indéfiniment en remplissant le plan de Conway de lignes horizontales vivantes et mortes alternées. Celles-ci sont limitées par 4 lignes diagonales se déplaçant précisément à la vitesse c/2.

Cette structure remarquable réalise donc la vitesse de croissance la plus élevée possible.